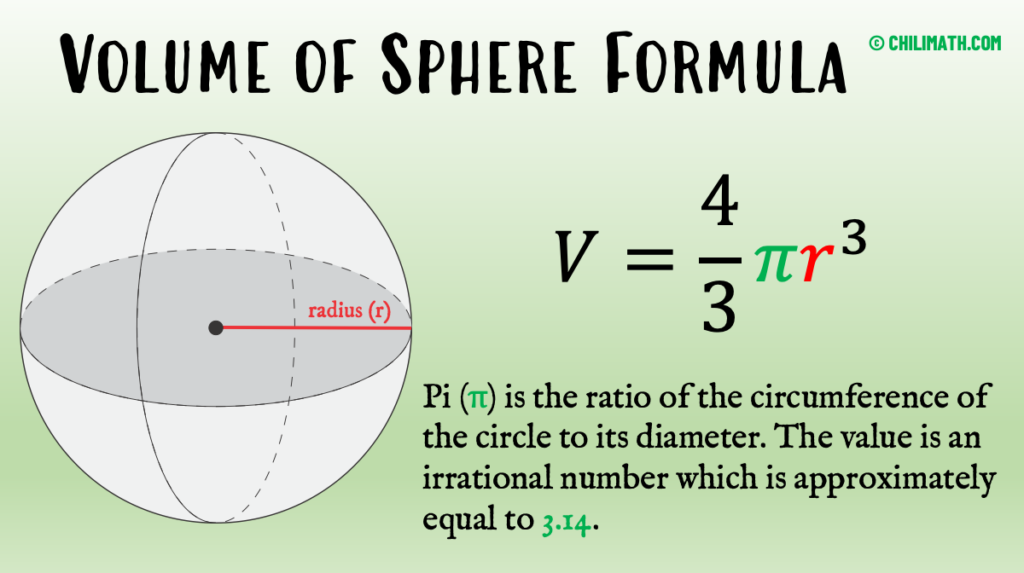
You will find ten (10) practice problems below regarding the sphere’s volume. This set of problems should provide you enough practice on how to use the formula to find volume of the sphere.
Use the formula below as a guide. Good luck!
Problem 1: Find the volume of a sphere that has a radius of [latex]5[/latex] yards. Use [latex]\pi=3.14[/latex]. Round your answer to the nearest tenth.
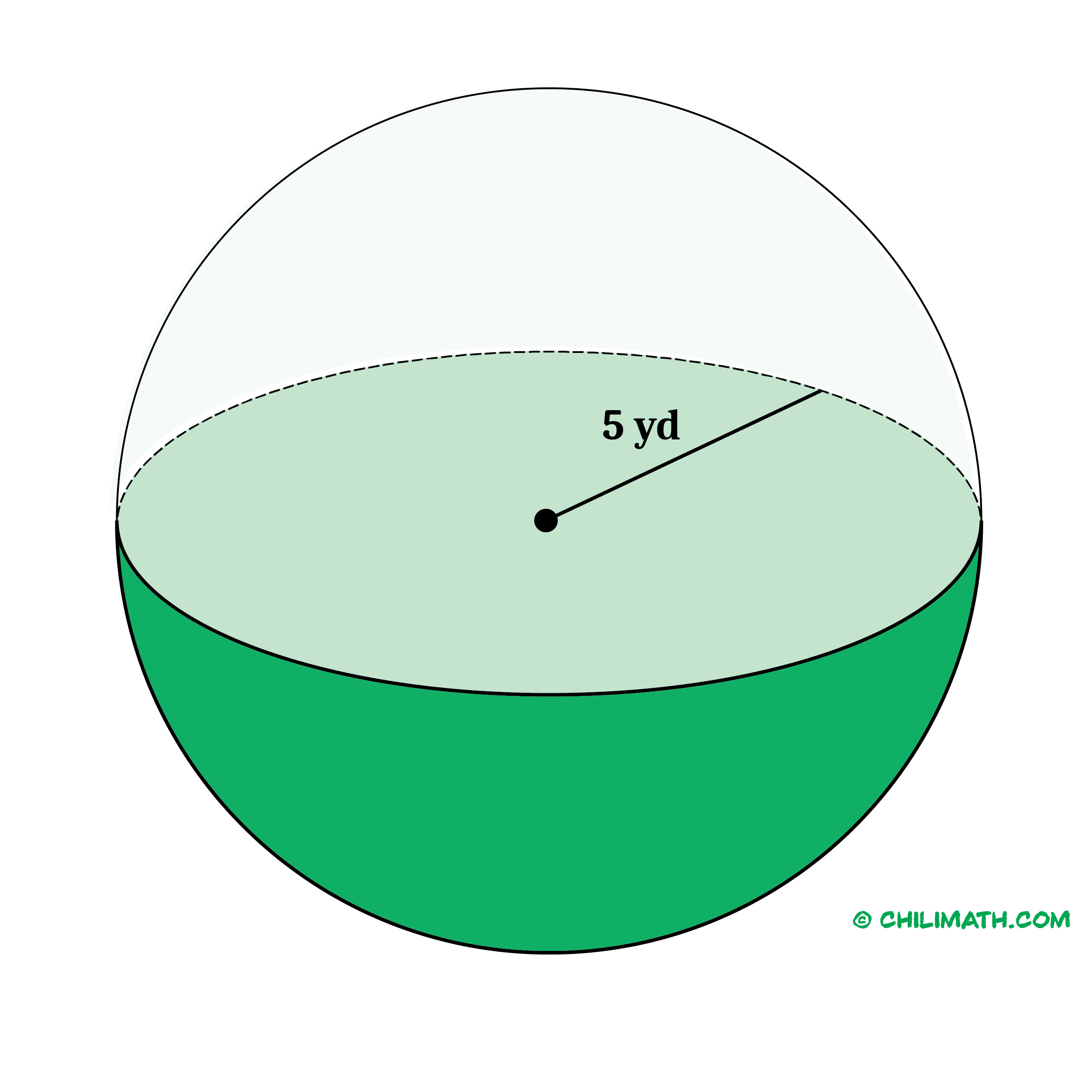a green sphere with a radius of 5 yards" width="2500" height="2500" />
Therefore, the volume of the sphere is approximately [latex]523.3[/latex] [latex]\text^3[/latex].
Problem 2: The radius of a sphere is [latex]1.5[/latex] centimeters. What is its volume? Use [latex]\pi=3.1416[/latex]. Round your answer to the nearest hundredth.
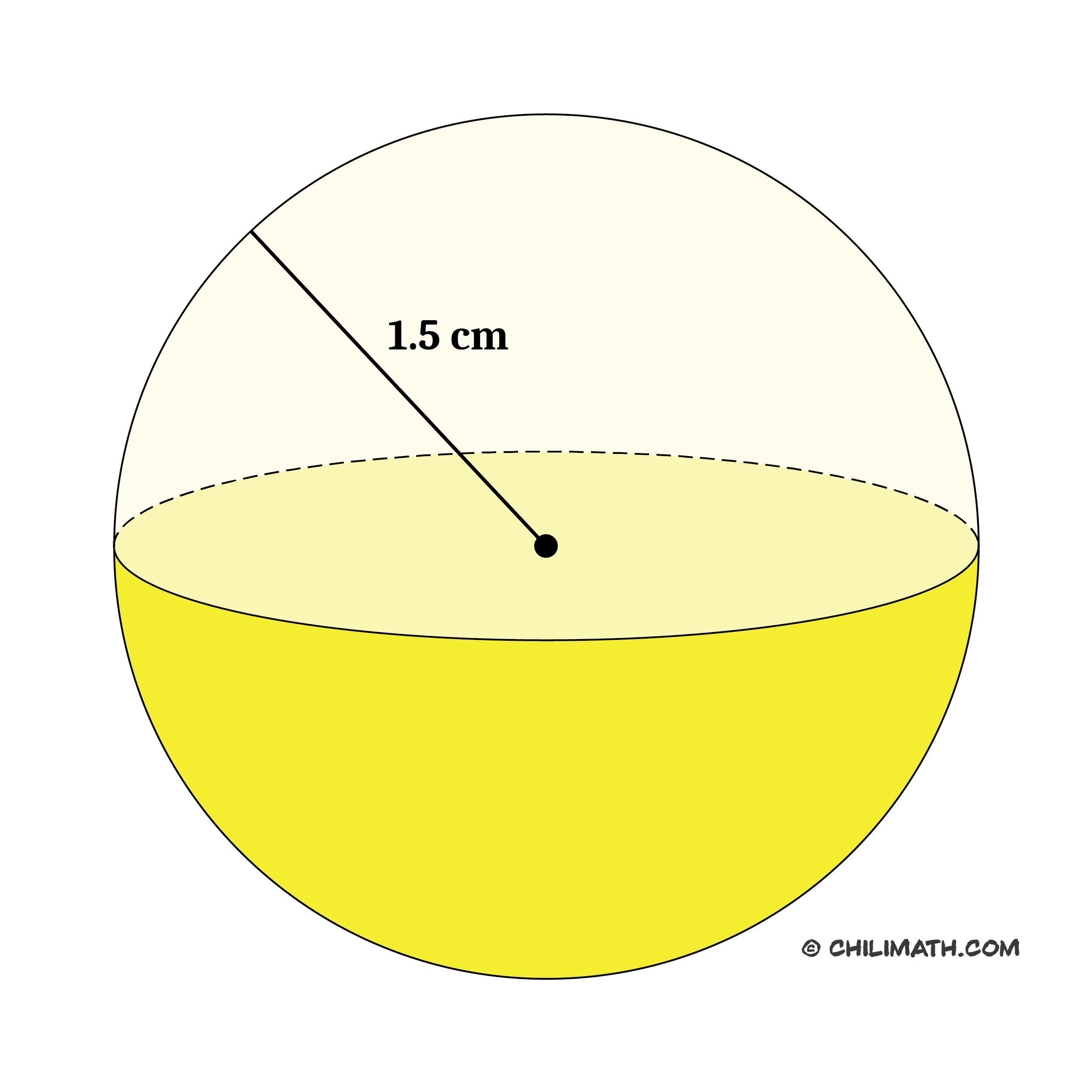
Therefore, the volume of the sphere is approximately [latex]14.14[/latex] [latex]\text^3[/latex].
Problem 3: Calculate the volume of a sphere with a radius of [latex]8[/latex] inches. Use [latex]\pi=22/7[/latex]. Round your answer to the nearest whole number.
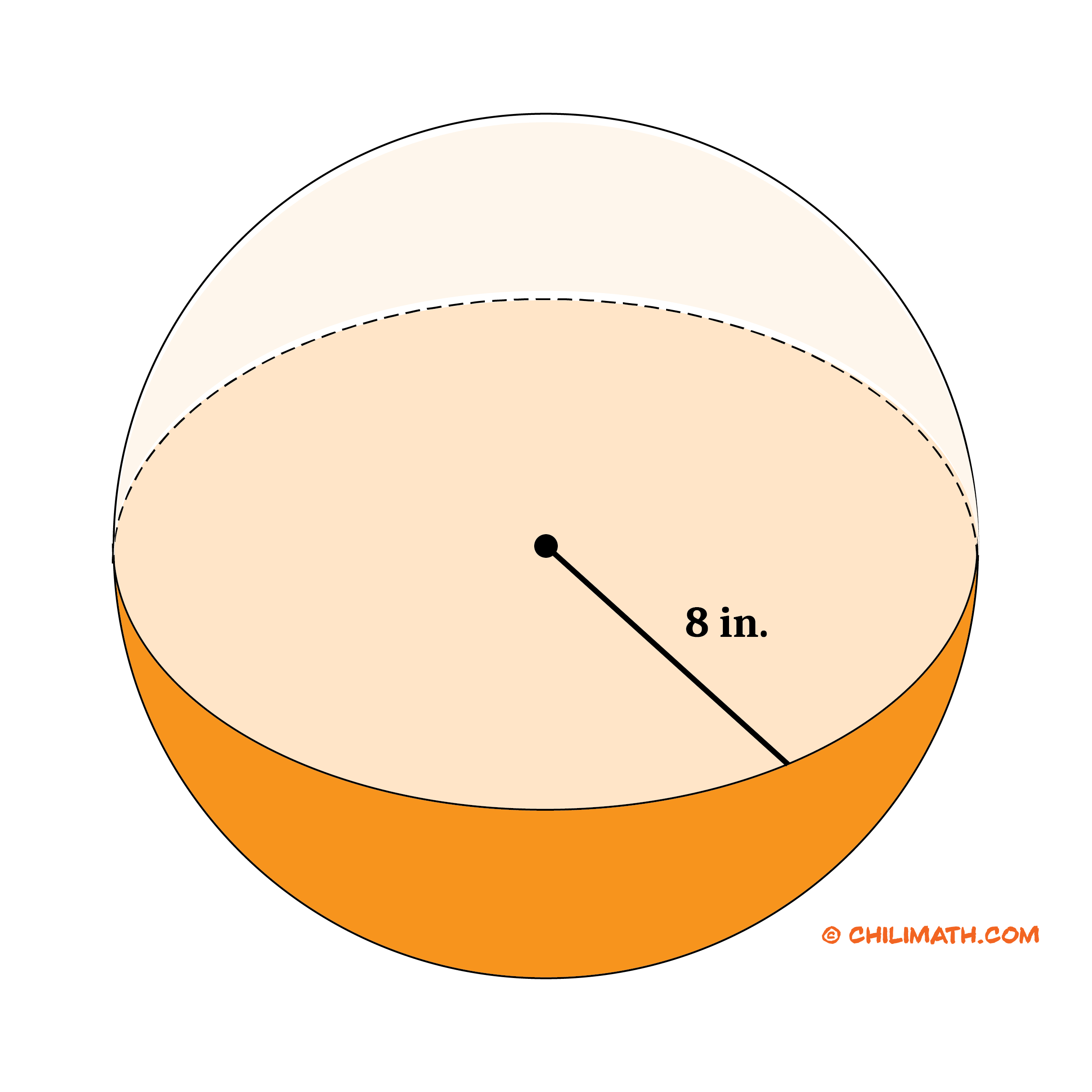of 8 inches" width="2500" height="2500" />
Therefore, the volume of the sphere is approximately [latex]2,146[/latex] [latex]\text^3[/latex].
Problem 4: Determine the volume of a sphere that has a diameter of [latex]14[/latex] meters. Use [latex]\pi=3.14[/latex]. Round your answer to the nearest hundredth.
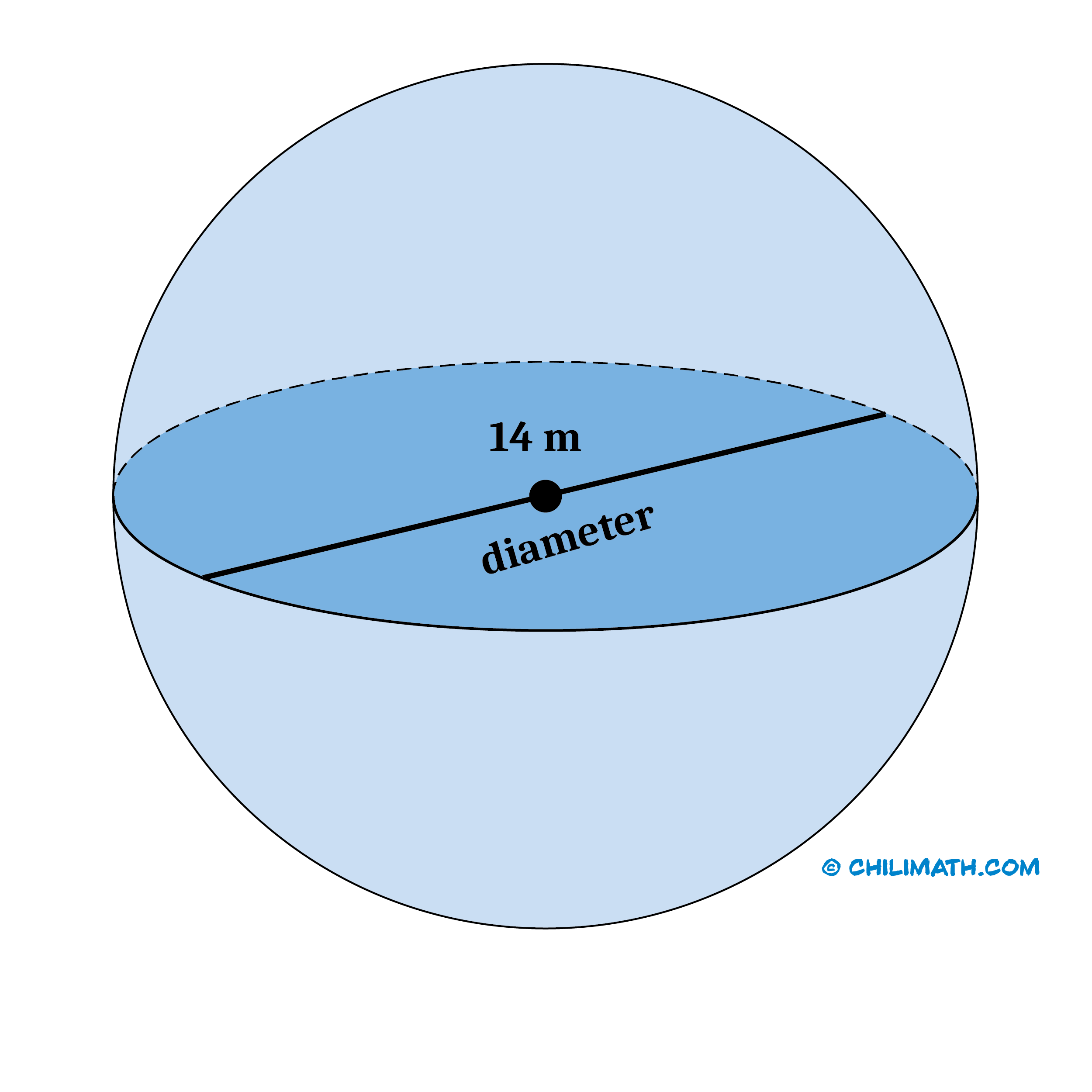of 14 meters" width="2500" height="2500" />
Therefore, the volume of the sphere is approximately [latex]1,436.03[/latex] [latex]\text^3[/latex].
Problem 5: If the diameter of a sphere is [latex]7[/latex] feet, what is its volume? Use [latex]\pi=3.1416[/latex]. Round your answer to the nearest thousandth.
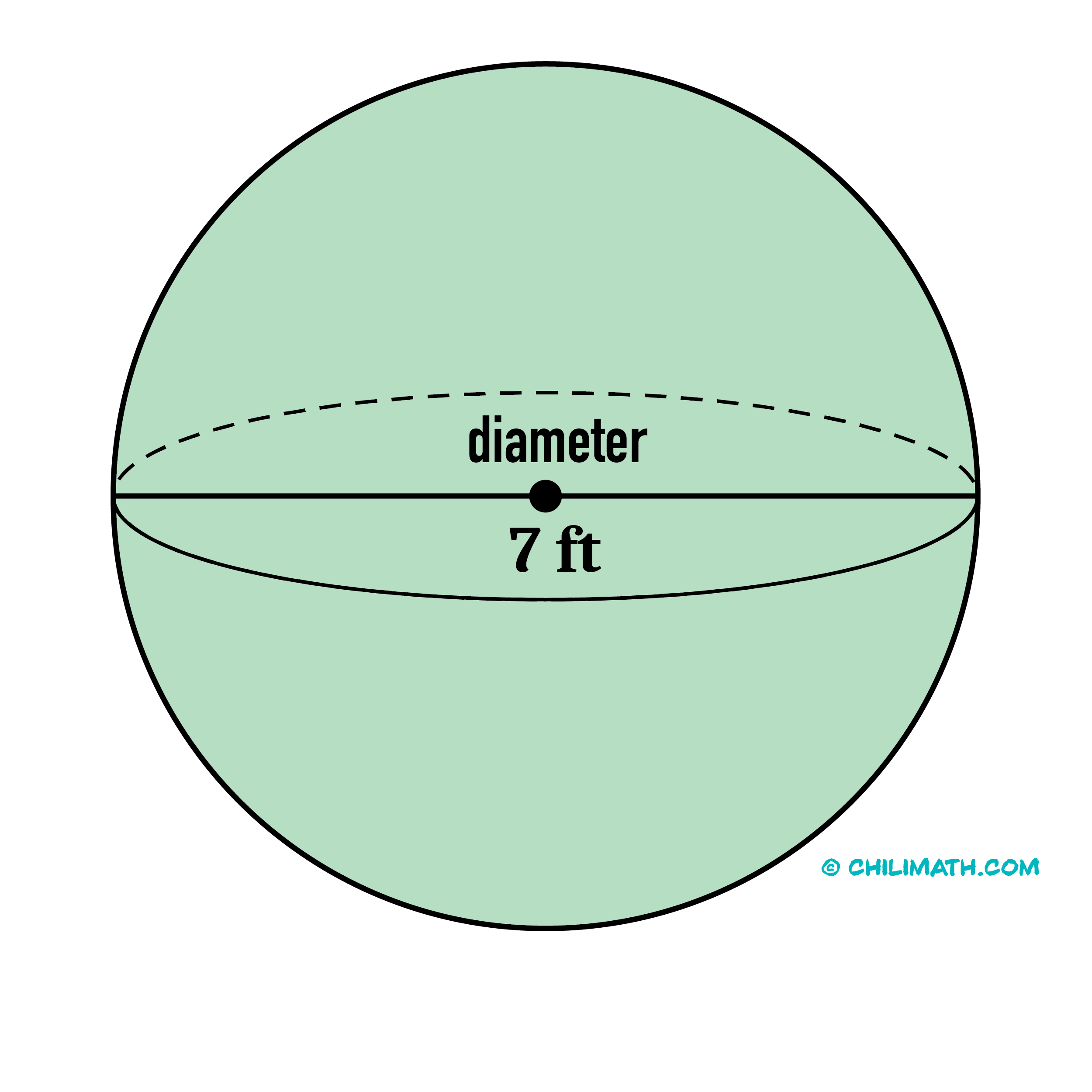diameter of 7 feet" width="2500" height="2500" />
Therefore, the volume of the sphere is approximately [latex]179.595[/latex] [latex]\text^3[/latex].
Problem 6: Find the volume of a sphere whose diameter is [latex]10.5[/latex] centimeters. Use [latex]\pi=22/7[/latex]. Round your answer to the nearest whole number.
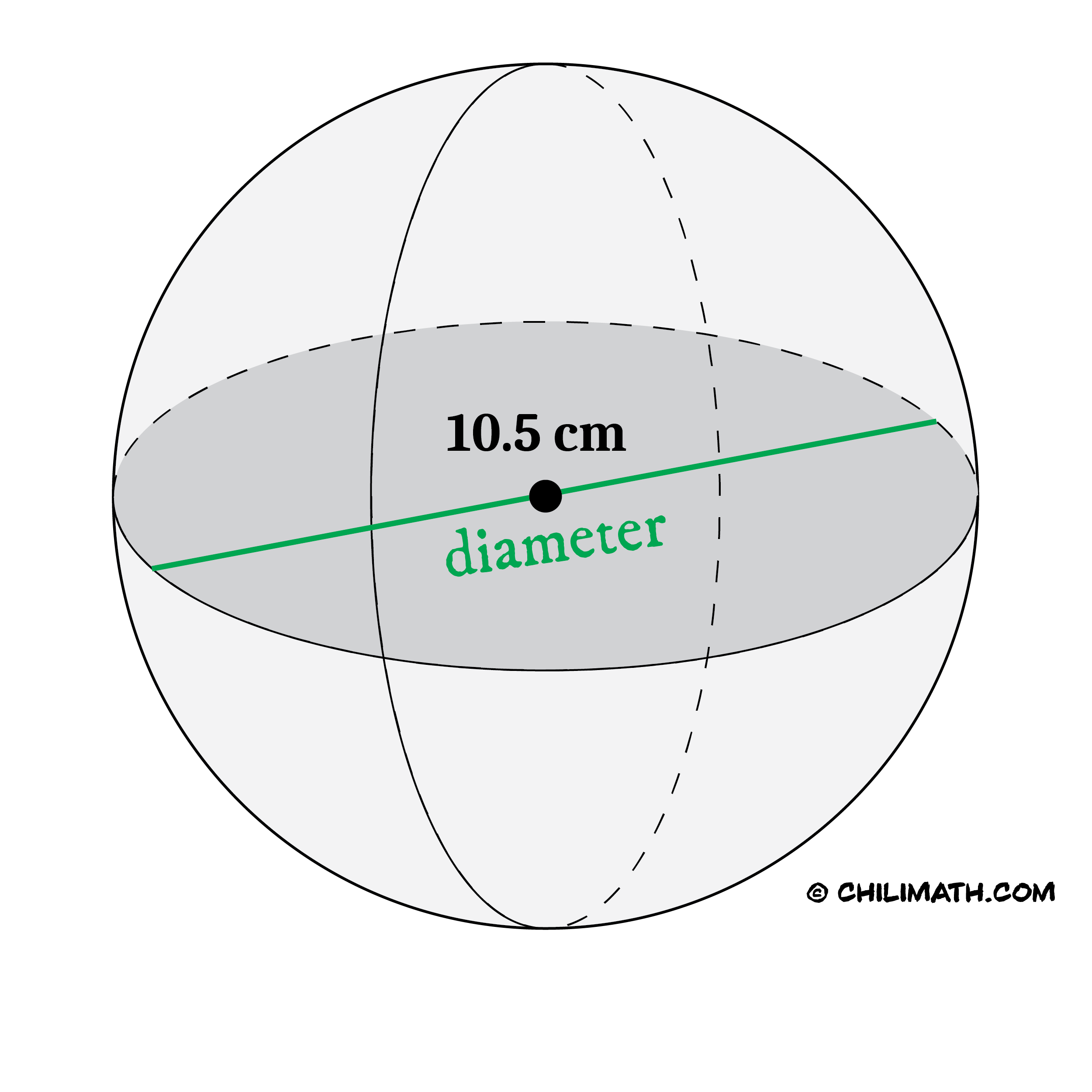
Therefore, the volume of the sphere is approximately [latex]606[/latex] [latex]\text^3[/latex].
Problem 7: The volume of the sphere is [latex]3,719[/latex] cubic kilometers. What is the radius of the sphere? Round your answer to the nearest hundredth. Use [latex]\pi=3.14[/latex].
Therefore, the radius of the sphere is [latex]9.61[/latex] [latex]\text[/latex].
Problem 8: Given that the volume of the sphere is [latex]1,000[/latex] cubic inches. Calculate its radius. Round your answer to the nearest tenth. Use [latex]\pi=22/7[/latex].
Therefore, the radius of the sphere is [latex]6.2[/latex] [latex]\text[/latex].
Problem 9: The surface area of a sphere is [latex]5,544[/latex] [latex]\text^2[/latex]. Find the volume of the sphere. Use [latex]\pi=22/7[/latex] as an approximation.
Find the radius of the sphere using the surface area formula.
\begin SA &= 4\pi \\ \\ 5,544 &= 4\left( \over 7>> \right) \\ \\ 5,544\left( 7 \right) &= 4\left( \right) \\ \\ 38,808 &= 88 \\ \\ \over > &= \\ \\ 441 &= \\ \\ \sqrt &= r \\ \\ 21 &= r \\ \\ \end
That means, the radius of the sphere is [latex]21[/latex] [latex]\text[/latex].
Use the radius from previous step to determine the volume of the sphere.
Therefore, the volume of the sphere is [latex]38,808[/latex] [latex]\text^3[/latex].
Problem 10: If the surface area of a sphere is [latex]9,856[/latex] [latex]\text^2[/latex], what is its volume? Round you answer to one decimal place. Use [latex]\pi=22/7[/latex] as an approximation.
Answer \begin SA &= 4\pi \\ \\ 9,856 &= 4\left( \over 7>> \right) \\ \\ 9,856\left( 7 \right) &= 4\left( \right) \\ \\ 68,992 &= 88 \\ \\ \over > &= \\ \\ 784 &= \\ \\ \sqrt &= r \\ \\ 28 &= r \end
That means the radius of the sphere is [latex]28[/latex] [latex]\text[/latex].
Now use the value of the radius to calculate the volume of the sphere.
Therefore, the volume of the sphere is [latex]91,989.3[/latex] [latex]\text^3[/latex].
You might also like these tutorials:
